Le parabole

Nota: ho scritto questo post per mio cugino che deve affrontare l'interrogazione di matematica, ma a scuola gli insegnano solo le formule a memoria senza nemmeno visualizzarne il significato e i poveri alunni si sentono persi e finiscono con l'odiare la matematica, mentre invece dovrebbero odiare solo la professoressa. Evidentemente ci sono molti insegnanti che non sono degni della cattedra su cui sono stati posti.

La parabola si ottiene dal cono. Quindi prima dobbiamo capire cos'è un cono. Immaginate un cono come quello del gelato, ma infinito (un gelato quindi infinitamente grande!). Un cono è un solido di rotazione generato da una semiretta fissa nel suo vertice (detta appunto "generatrice") ma libera di ruotare a 360° attorno ad un asse fisso di rotazione passante per il suo vertice pur mantenendo sempre la stessa angolazione rispetto all'asse. Il modo più semplice per rendersene conto è provare a far ruotare il vostro dito indice puntato in alto attorno ad un asse immaginario verticale. Oppure potete pensare di ruotare un triangolo rettangolo attorno ad uno dei suoi lati preso come asse di rotazione. Anche se questo genera solo un cono finito, come (purtroppo!) quello del gelato, di altezza cioè non infinita ma pari alla lunghezza del lato del triangolo mantenuto fisso durante la rotazione. Il lato opposto a quello considerato come asse sarà la semiretta generatrice, mentre il terzo descriverà il piano di basedel cono. Questo cono viene detto retto, perché l'altezza e il piano di base sono perpendicolari. Viene anche detto circolare perché la base è un circolo. Esistono anche coni obliqui ed ellittici, ma se parliamo di cono senza dire altro di solito si intende un cono circolare retto, tipo quello del gelato.

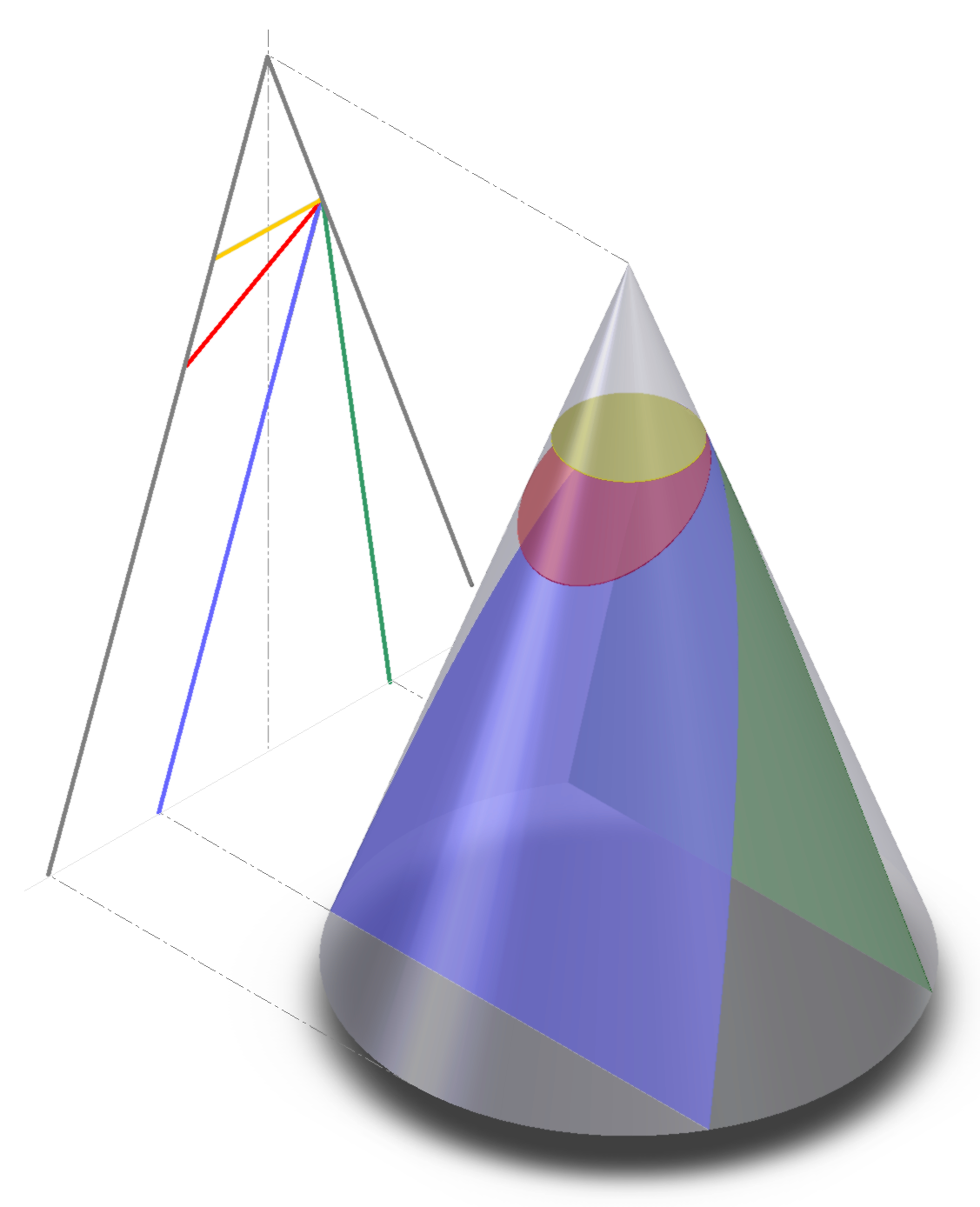
Preso un cono circolare retto, immaginate di tagliarlo nettamente con un coltello. Ebbene se lo tagliate in modo parallelo al suo piano di base (al di sotto del vertice ovviamente!) il bordo della superficie di taglio (in giallo nella figura qui sotto) sarà ovviamente una circonferenza perfetta ed otterete un tronco di cono su cui vi potete sedere. Inclinando però sempre di più il coltello (o piano di taglio), otterrete degli ellissi, sempre più schiacciati o "eccentrici" (come quello disegnato in rosso), finché se arrivate a tagliare in modo perfettamente parallelo alla semiretta generatrice, l'ellisse sarà di eccentricità infinita e non è più una figura chiusa. Esso diventa una parabola (disegnata in blu). Andando oltre con l'inclinazione si ottiene una iperbole (in verde) (in realtà un solo ramo. Se il cono fosse doppio, generato da una retta anziché una semiretta, si otterrebbero due rami). Sono stati i greci nel 200 a.C. a studiare per primi queste sezioni coniche. La parabola ha la caratteristica forma ad U, mentre la iperbole ha un forma pure ad U, ma una U più aperta ma è doppia, nel senso che è formata in realtà da due U una sopra l'altra e una di esse rovesciata.

Nel 17esimo secolo Isacco Newton ha scoperto che le sezioni coniche rappresentano i moti nel nostro sistema solare. In particolare cerchi ed ellissi con vari raggi e inclinazioni rappresentano quelli dei corpi legati al sole. Così i pianeti, gli asteroidi e le comete che fanno parte del sistema solare si muovono secondo orbite quasi circolari (Mercurio e Marte hanno la maggiore eccentricità, Venere e Nettuno la minore). Mentre invece una cometa di passaggio può seguire una traiettoria parabolica o iperbolica.

La parabola è importante anche perché rappresenta il moto idealizzato di un proiettile o una palla di cannone o anche un sasso che invece di essere lasciato cadere in verticale viene lanciato in una direzione non verticale, come quando si tirano i sassi nel mare. La cosa non stupisce se si accetta che la stessa forza che fa muovere i pianeti attorno al sole fa anche cadere le pietre sulla terra o fa andare in circolo un satellite. Fu Galileo Galilei a scoprire sperimentalmente questo fatto tra il 1604 e il 1608. Prima di Galilei si credeva che lanciando una pietra essa si muovesse di moto rettilineo e poi improvvisamente cadesse a terra, esaurito l'"impeto" della forza di chi l'aveva lanciata. Dal momento che oggetti lanciati su brevi distanza come le pietre che si gettano a mare hanno un moto parabolico a forma di U molto larga, nessuno si era accorto che il moto era effettivamente una parabola e non due rette perpendicolari. Però ai tempi di Galilei esistevano (purtroppo ma anche per fortuna della scienza) già i cannoni ed era chiaro che le palle di cannone che venivano gettate a grande distanza causa il grande impulso impresso dall'esplosione della polvere da sparo seguivano un moto ad U, una curva arrotondata e non due rette consecutive.

Ma le palle di cannone erano così veloci e Galilei non aveva alcun mezzo per misurare il percorso del proiettile e determinare di che tipo di curva si trattava. Con la tecnologia di oggi sarebbe facile. Basta una luce stroboscopica come quella delle discoteche e una telecamera e si può guardare il filmato a rallentatore. Ma Galilei non aveva nemmeno un orologio da polso, perché gli orologi meccanici non erano stati ancora inventati! Come ha fatto allora Galileo a capire e dimostrare matematicamente che il moto di un proiettile era parabolico? Ha dovuto far ricorso ad un esperimento molto ingegnoso.

Ha preso un piano inclinato e l'ha messo sul bordo di un tavolo. Poi ha preso una di bronzo inchiostrata e l'ha fatta rotolare lungo il piano. Cadendo in terra, dove aveva posto dei fogli di carta, la pallina ha lasciato un segno nel punto di caduta. Per far sì che la pallina fosse lanciata di traverso e non cadesse verticalmente oltre il bordo del tavolo, Galilei ci ha messo una specie di lamiera deflettore. Variando la velocità della pallina e l'altezza del tavolo, Galilei fu in grado di determinare sperimentalmente che il moto era una parabola.

Infatti detta x la distanza orizzontale percorsa dalla pallina, che può essere misurata grazie alla macchia d'inchiostro lasciata, ed y l'altezza del tavolo, risulta dall'analisi dei dati di tante misure che questi numeri sono sempre legati dalla relazione:

y=a x ^ 2

Dove a è un numero fisso. Se andiamo a disegnare in un diagramma cartesiano la curva che si ottiene congiungendo i punti (x,y) ottenuti assegnando valori abbastanza vicini di x a seconda della nostra scala e precisione di disegno e calcolando x con la suddetta formula, vediamo che ha la forma di una parabola. Questa parabola ha il vertice in (0,0). Se aggiungiamo un numero c costante alla formula:

y=a x ^ 2 + c

si ottiene uno spostamento verticale. Allora il vertice sarà (0,c), infatti per ponendo x=0 nella formula sopra si ottiene stavolta y=c e la posizione orizzontale del vertice non può cambiare se spostiamo la parabola solo verticalmente. Se invece la spostiamo solo orizzontalmente, allora quale sarà la formula matematica? E' facile, al posto della x nell'equazione:

y=a x ^ 2

bisogna mettere (x-s) dove s è l'entità dello spostamento. Se s è un numero positivo, ad es. 1, lo spostamento è di s unità a destra, mentre se è negatio è di s unità a sinistra, ma può essere anche un numero decimale per spostamenti arbitrariamente precisi. Si ottiene quindi:

y=a (x-s)^2

Ma (x-s)^2=(x-s)*(x-s)=x^2 - s x - s x + s^2=x^2 - 2s x + s^2 Ricordando che c'è anche a che moltiplica tutti i termini, la formula diventa:

y=a x ^ 2 - 2as x + a s^2

Il vertice della parabola sarà stato ovviamente spostato anch'esso di s. Le sue coordinate sono (s,0) (infatti ponendo x=s in una delle due formule precedenti viene 0, provare per credere). Vediamo adesso cosa succede se si combinano i due spostamenti. Basta che aggiungiamo c alla formula di prima:

y=a x ^ 2 - 2as x + a s^2 + c

Il vertice di questa parabola sarà (s,c).

Se uno si trova di fronte ad una formula del tipo:

y=i x^2 + j x + k

e vuole sapere qual'è il vertice della parabola, può allora furbescamente porre:

i = a
j = - 2 a s
k = a s^2 + c

essendo i,j,k numeri noti, si tratta di determinare s e c in funzione di loro e il vertice sarà appunto (s,c). Siccome i = a, la seconda equazione diventa:

j = - 2 i s

da cui si determina

s = - j / 2 i

Sostituendo i per a e questa espressione di s nella terza si ha:

k = i (- j / (2 i))^2 + c

da cui si determina c in funzione di i, j, k noti:

k = i j^2 / 4 i^2 + c
si semplifica la i a numeratore e denominatore
k = j^2 / 4 i + c

c = k - j^2 / 4 i

Quindi in conclusione, data una parabola di equazione:

y=i x^2 + j x + k

abbiamo dimostrato che il vertice ha coordinate:

(- j / 2 i, k - j^2 / 4 i)

Se uno non si ricorda la formula a memoria (io non la ricordo), può rifarsi da se la dimostrazione e ritrovarla. L'importante non è sapere le formule, ma saperle dimostrare. Si possono fare tutti gli esempi numerici e gli esercizi che uno vuole, ma se uno sa fare la dimostrazione della formula, non ha certo bisogno di esercizi, che sono meri calcoli noiosi. Comunque eccone uno:

x = y^2 - 3 y + 2

Non fatevi confondere dal fatto che x e y qui sono invertiti. Vale sempre la stessa formula, ma ovviamente le coordinate del vertice saranno pure invertite. Qui:

i = 1
j = -3
k = 2

Invece di

(- j / 2 i, k - j^2 / 4 i)

le coordinate del vertice saranno

(k - j^2 / 4 i, - j / 2 i)

facendo i conti risulta:

(2 - (-3)^2 / 4 1, - (-3) / 2 1)

(2 - 9/4, 3/2)

(8/4 - 9/4, 3/2)

(-1/4, 3/2)

Ma i numeri non sono la matematica. La matematica è fatta di dimostrazioni e di relazioni tra i suoi oggetti. I numeri sono solo conti, li sa fare anche un computer e meglio di noi. Sapere far di conto non significa sapere la matematica e nemmeno essere bravo in matematica.